Naar een duurzame toekomst: ruimteverkenning als motor voor aardse duurzaamheid
Ruimteverkenning doet veel meer dan onze kennisgrenzen verleggen. Het speelt een cruciale rol in het bevorderen van duurzaamheid op aarde.
Ruimteverkenning doet veel meer dan onze kennisgrenzen verleggen. Het speelt een cruciale rol in het bevorderen van duurzaamheid op aarde.
Het extraheren, invriezen en opnieuw transplanteren van plakjes hormoonproducerend eierstokweefsel kan de menopauze uitstellen, al hebben sommige experts bedenkingen over de werking of het nut ervan.
Als er te veel CO2 in de atmosfeer zit, waarom halen we die er dan niet gewoon uit? Bomen en planten kunnen dat, dus moet het toch ook mogelijk zijn met technologie? Het kan inderdaad met Direct Air Captioning (DAC). Critici menen dat er efficiëntere manieren zijn om het opwarmen van de aarde te beperken tot 1,5°C. Binnen de plannen van de EU is de techniek wel een middel om in 2050 netto nul uitstoot te bereiken.
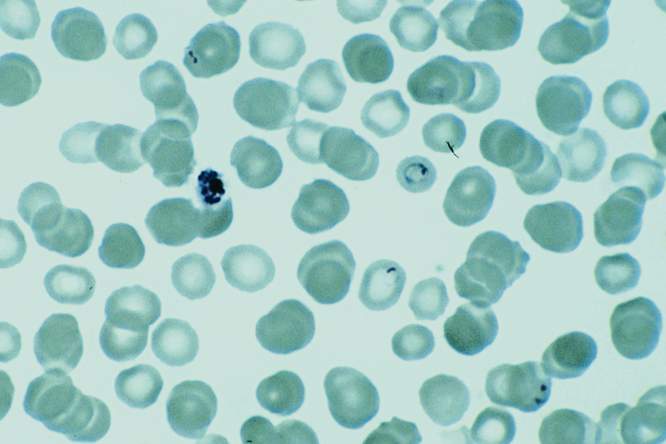
Op 25 april, Wereld Malariadag, besteden we extra aandacht aan wetenschap die werkt aan effectieve medicijnen tegen de ziekte. Mathijs Mutsaers is onderzoeker aan het Instituut voor Tropische Geneeskunde. Zijn team ontwikkelde een methode om snel en goedkoop resistentie tegen bestaande medicijnen op te sporen.
Wie in het bos gaat wandelen, moet al maanden door het slijk ploeteren. Zal de overvloedige regen gevolgen hebben voor de natuur? Botanicus Wouter Van Landuyt van het Instituut voor Natuur- en Bosonderzoek (INBO) maakt zich voorlopig geen zorgen. ‘Natte winters zijn de normale gang van zaken.’